C. 고유값 분석
구조물은 형상, 재질 및 경계조건에 따라 고유진동 특성을 가집니다. 고유진동 특성이란, 외부로부터의 어떠한 자극을 받지 않는 자유로운 진동상태를 의미합니다. 이러한 특성을 찾는 해석방법을 모드해석, 고유치해석 또는 자유진동해석이라고 합니다. 고유치해석을 통해 구조물의 고유진동수와 이에 대응하는 고유모드를 알 수 있습니다. 고유진동수는 단위 시간당 얼마나 빨리 반복되는가의 정도를 나타내고, 고유모드는 주어진 구속상태에서 자유로이 변형될 수 있는 형상을 의미합니다.
구조물의 고유진동특성은 외력의 영향을 받지 않는 상태의 비감쇠자유진동(undamped free vibration)으로 부터 얻을 수 있습니다. 비감쇠자유진동이기 때문에 감쇠행렬(damping matrix)과 외력이 0인 동적평형방정식을 만들 수 있고, 변위벡터 u(t)를 변위형상함수와 시간 함수의 곱으로 가정해 고유진동수와 고유모드를 계산할 수 있습니다. 다자유도시스템은 강성과 질량이 행렬 형태라는 점을 제외하고 단자유도시스템과 동일한 방식으로 계산할 수 있습니다.
가장 작은 고유진동수를(고유주기는 가장 긴) 구조물의 기본고유진동수(fundamental natural frequency)라고 하며, 구조물의 동적 특성을 나타내는 중요한 척도로 사용됩니다. 고유진동수를 알면 그에 상응하는 모드형상(자유진동모드, 진동모드, 모드)을 구할 수 있습니다. 고유값의 주요 문제인 자유진동모드는 상대적인 값들의 조합으로 그 형상만을 나타내며, 임의의 값으로 절대적인 크기를 가정합니다. 수치해석에서는 모드의 진폭을 임의의 값으로 사용하는 것이 불편하므로 일정한 기준에 따라 모드형상의 진폭을 결정하는 것을 권장하며, 이를 모드형상의 정규화, 얻어진 모드를 정규화 모드라고 합니다.
구조물의 해석 모델을 실제와 같게 만들수록 자유도는 무한정 늘어나게 됩니다. 구조물이 갖는 자유도 만큼 모드가 생기기 때문에, 자유도 개수만큼의 미지수를 갖는 연립미분방정식을 풀어야 하는 상황이 발생합니다. 따라서 효율적인 동해석을 위해서는 적절한 자유도를 선정해서 해석을 수행해야 하는데, 자유도를 줄이는 효과적인 방법 중에 하나가 구조물의 중요한 자유진동모드벡터(Eigenvector)를 이용하는 모드중첩(mode superposition method)입니다.
앞서 말했듯이, 구조해석 모델을 실제거동과 유사하도록 강성행렬(stiffness matrix)을 정확히 모형화하게 되면 그만큼 많은 자유도가 생기게 됩니다. 모드중첩은 이 자유도를 모두 동해석 시에 고려하는 것이 아니라, 동역학적으로 주요한 영향을 미치는 자유진동모드벡터 또는 리츠벡터(Ritz Vector)만을 해석에 포함시킴으로써 효율성을 증대시키는 방법입니다. 아래의 그림은 모드 중첩의 기본개념인고, 여러 개의 자유도를 갖는 구조물의 변형형상을 하나의 대표모드만으로도 표현할 수 있다는 것을 보여줍니다.
 그림. 동해석을 수행한 교량의 거동
그림. 동해석을 수행한 교량의 거동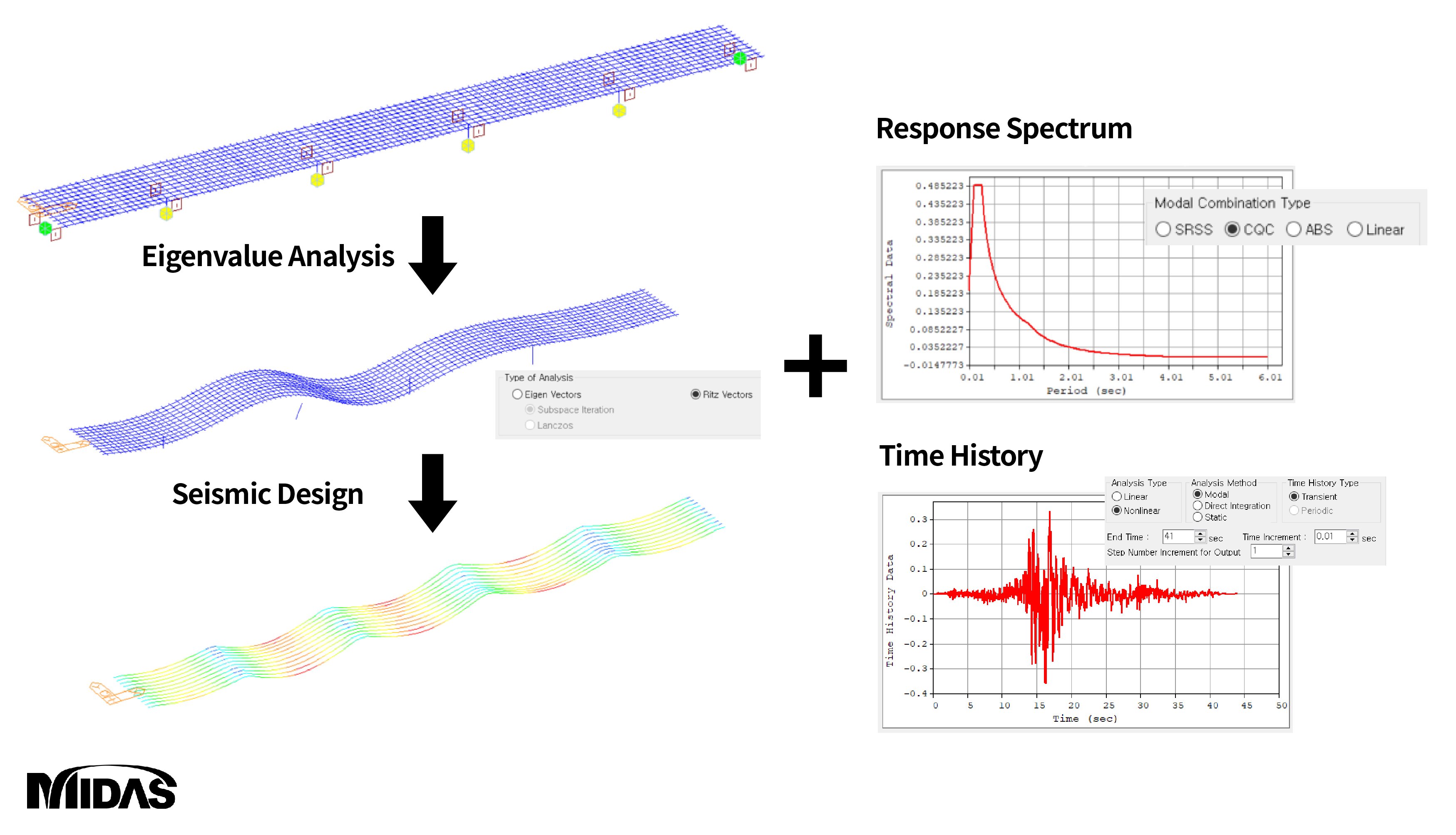
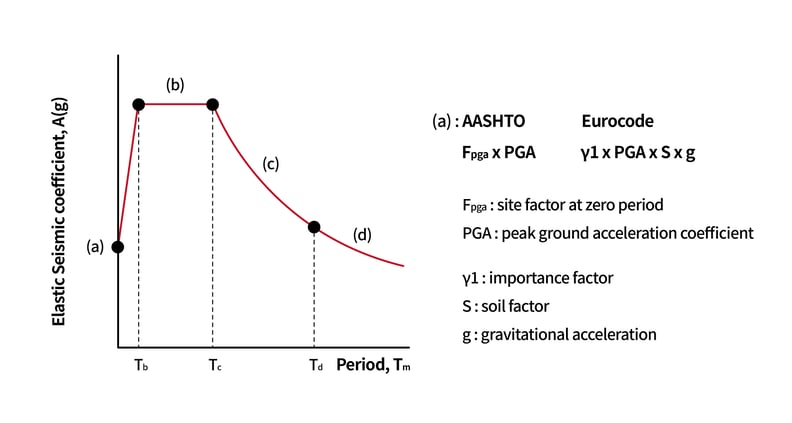 그림.
그림. 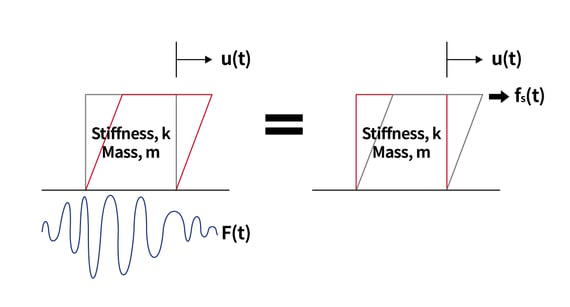 그림. 등가정적하중의 개략도
그림. 등가정적하중의 개략도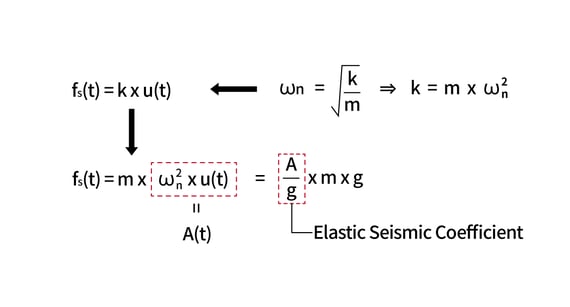 그림.
그림. 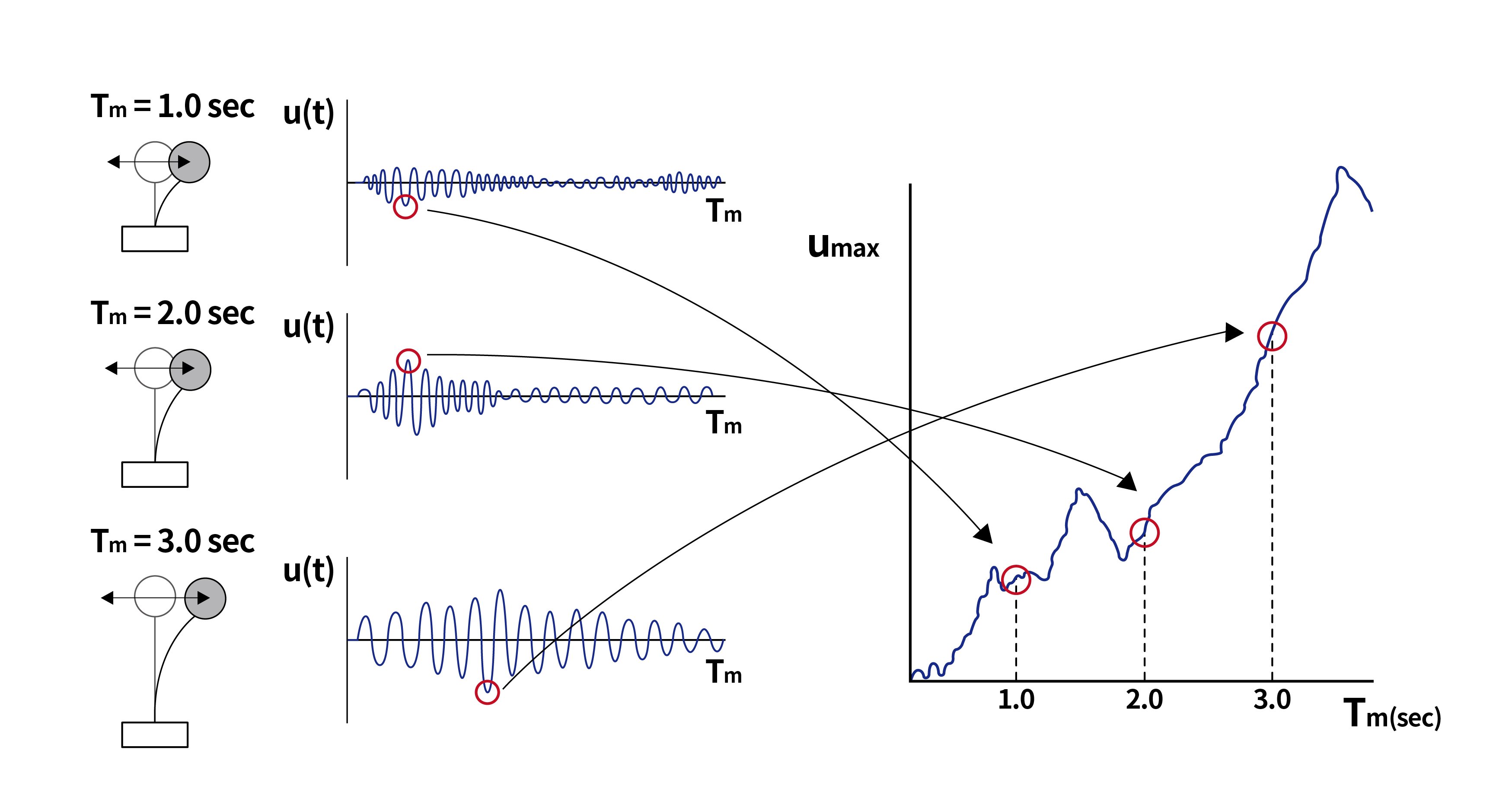 그림.
그림. 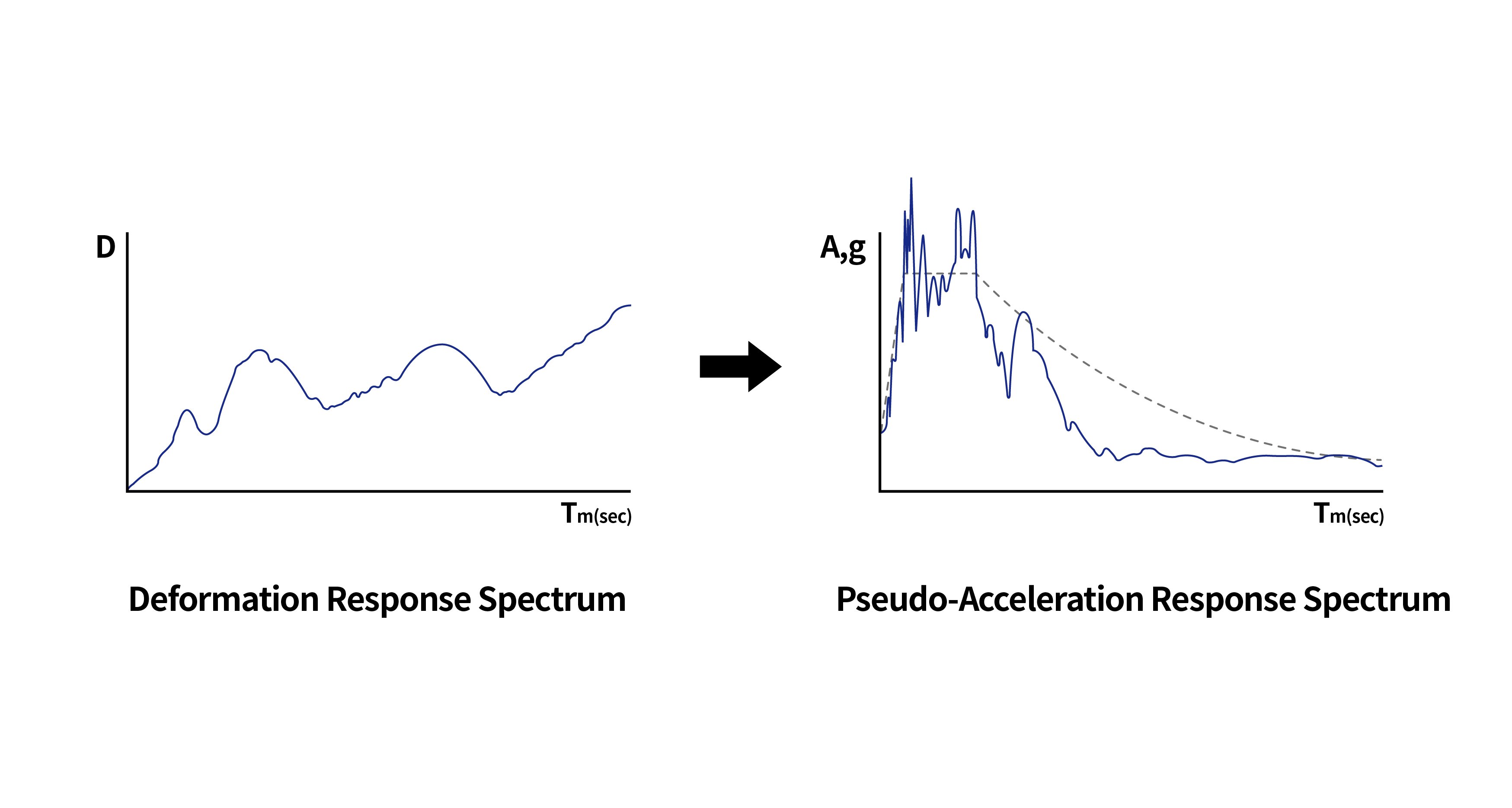
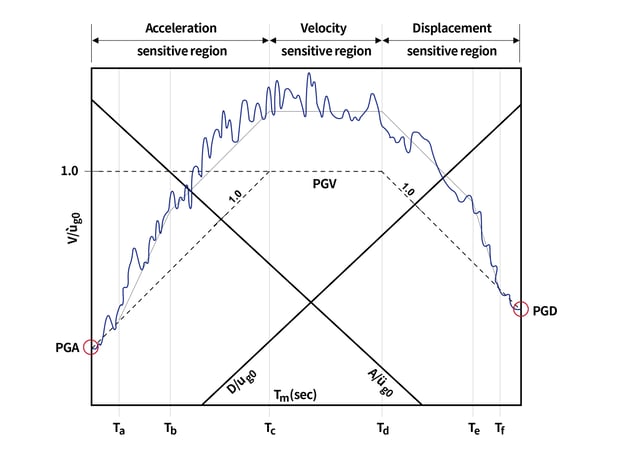 그림. 조합 D-V-A 응답 스펙트럼
그림. 조합 D-V-A 응답 스펙트럼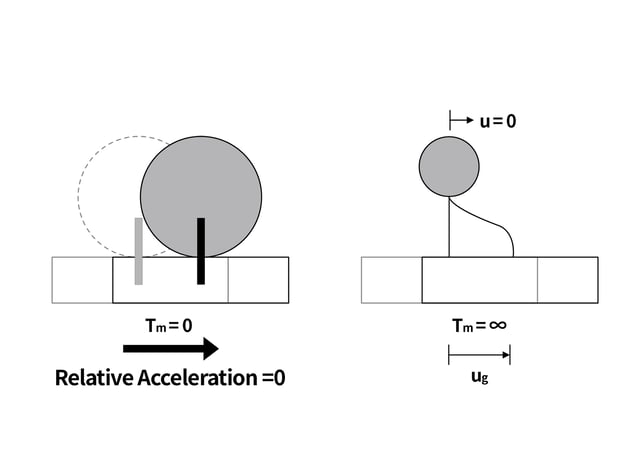
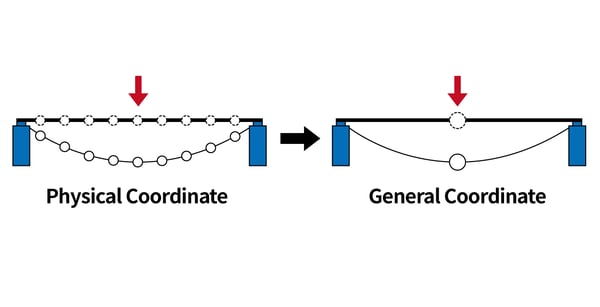
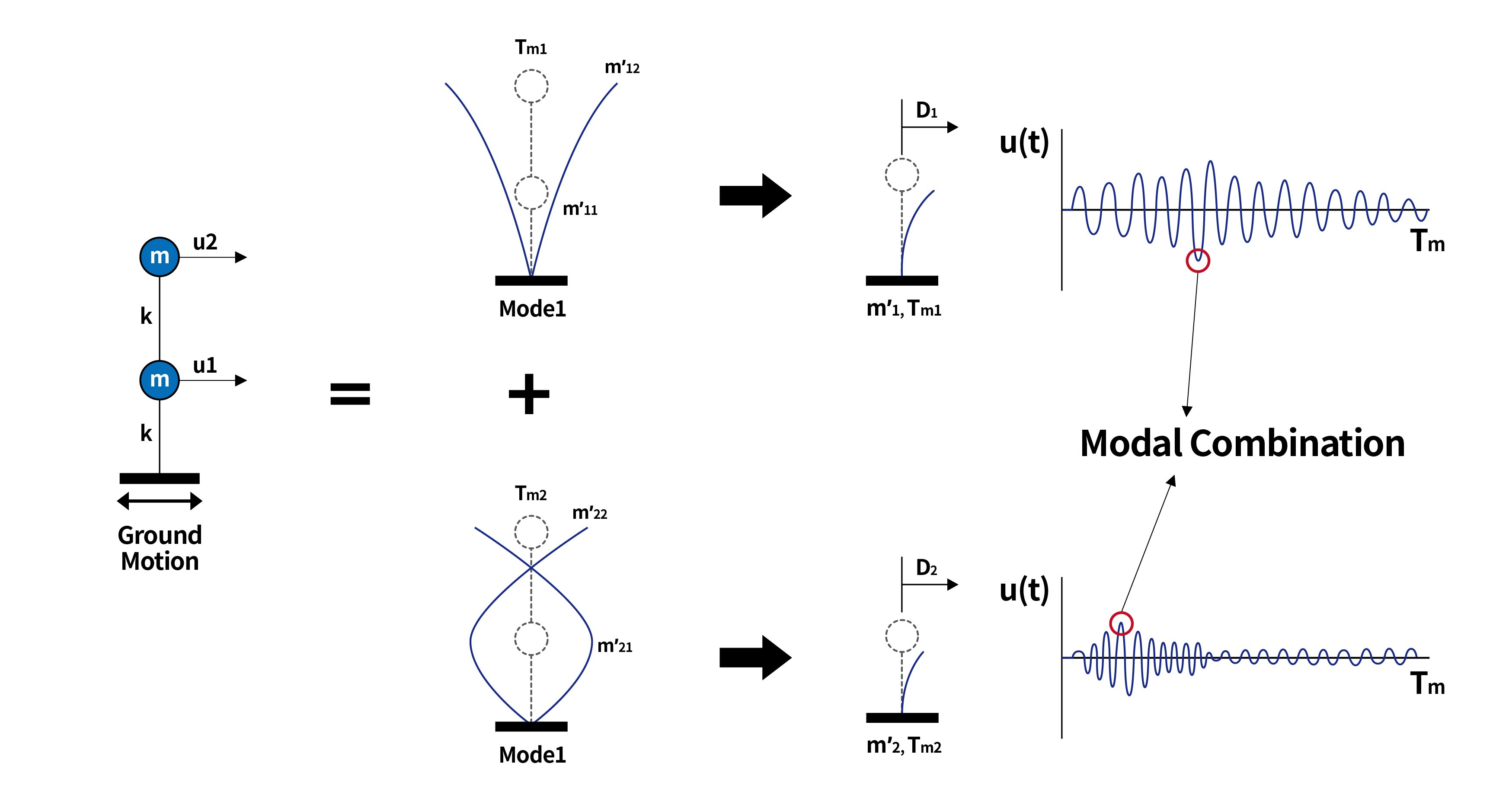
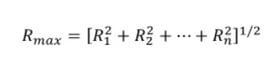
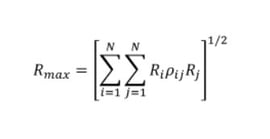
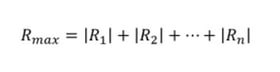
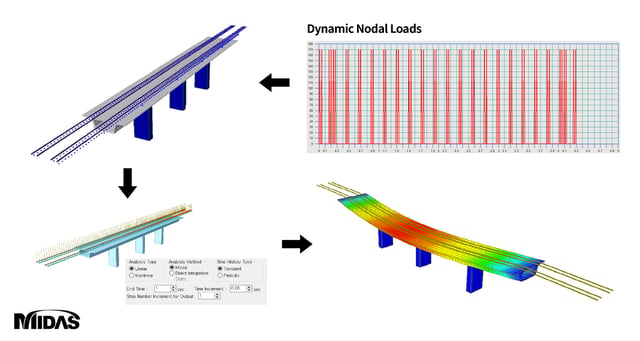 그림. 철도 교량의 동해석
그림. 철도 교량의 동해석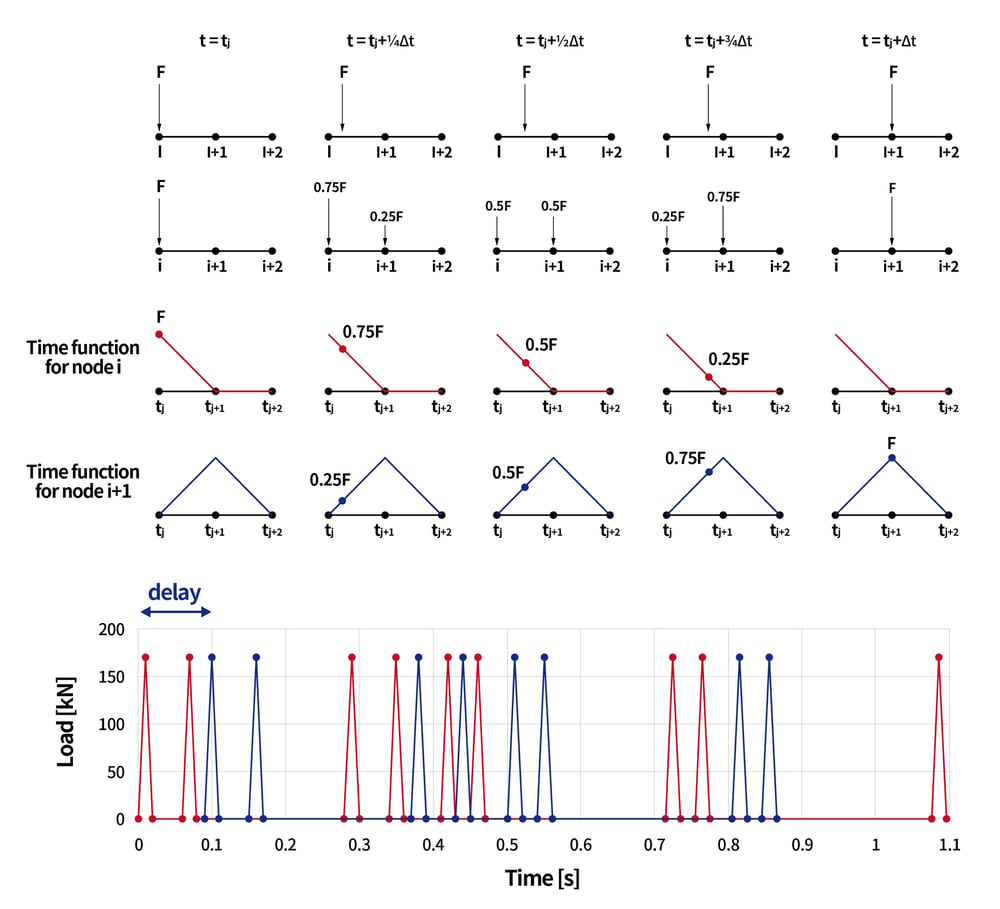 그림.
그림.